A modellrepülés elmélete (6)

Példa:

F1A modell összes felülete 34 dm²
ebből a szárny felülete 30,04 dm²

A felületi terhelést az összes felület alapján számítva

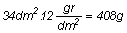
ha ugyanezt a súlyerőt csak a szárny felületére osztom el:

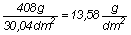
felületi terhelést kapunk. Ezért csökkentik a lehető legkisebbre a csillapítók felületét, és hogy mégis hatásos legyen, kiteszik a nagyon hosszú törzsek végére.

Az emelkedési szám

A merülősebesség (w) rendezése során keletkezett a gyökjel alatt a tört nevezőjében a

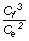
kifejezés amit “emelkedési szám”-nak nevezünk.

Ha adott polárgörbéhez a legkisebb merülési pontot nem csak szerkesztéssel hanem számítással is meg akarjuk kapni, a profil mérési eredményeit tartalmazó táblázatot kell elővenni. A szárnyszelvények tulajdonságait a kísérleti intézetek a C_f, a C_e és C_m tényezőkkel adják meg, amelyek az állásszögtől függően táblázatokban találhatók.

A táblázat a következő adatokat tartalmazza:

Adott oldalviszonyra (l = 10) átszámítva egyes állásszögekhez tartozó
C_f és
C_e értékei

Ezek alapján ki kell számítani a görbe rajzolásához szükséges értékeket.
Ezek a kiszámított értékek:

C_f/C_e és
C_f³/C_e²

ezután kell ezeket - az X tengelyen nem azonos léptékkel - de azonos Cf - hez tartozó adataikat külön görbeként közös diagramban ábrázolni.

(C_e² értékeit 10^-3-al kell szorozni ! - mert ez az érték a sok tizedesvessző utáni számjegy miatt táblázatba nem fért bele)

Ezekből az adatokból a következő jellegű görbéket kapjuk:

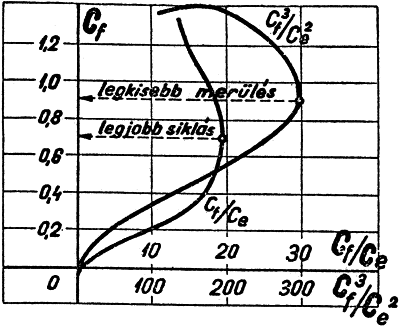
A C_f/C_e érték maximuma
a legjobb siklás pontja,

a C_f³/C_e² legnagyobb értéke
a legkisebb merülősebesség helyét

adja meg.

Ebből a diagramból is megállapítható hogy:

a legkisebb merülősebesség
valamivel nagyobb állásszög mellett érhető el, mint
a legjobb siklószám.

Ilyen számításokkal igazolható az az összefüggés is, hogy

Összefüggések

Az oldalviszony és az indukált ellenállás.

A harmadik rész az indukált ellenállással fejeződött be. Ebben a részben volt magyarázat a jelenségre, és két szárnyméret esetén számítottuk ki az indukált ellenállás nagyságát. A szárny oldalviszonya és az indukált ellenállás nagysága közötti összefüggés diagramban is megadható.

A C_y a felhajtóerő-tényező
a C_xi az indukált ellenállás tényezője

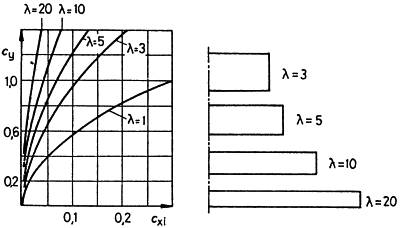
Az oldalviszony a szárnyszelvény polárgörbéjét is jelentősen befolyásolja. A 4. részben említett polárgörbék mindig végtelen oldalviszonyú szárnyakra vonatkoznak - de bármilyen polárgörbéhez meg kell adni a hozzá tartozó Reynolds számot is ! (Például a 4. részben közölt N 60 szelvénynél l = 5, Re = 84000)

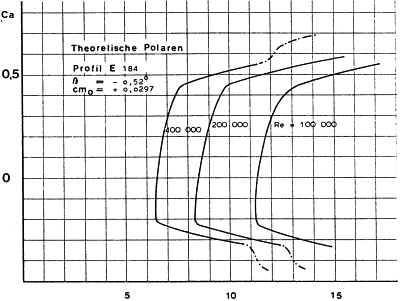
Az alábbi ábra egy E-385 szelvény görbéit adja meg különböző oldalviszony, de állandó Re =100 000 mellett.

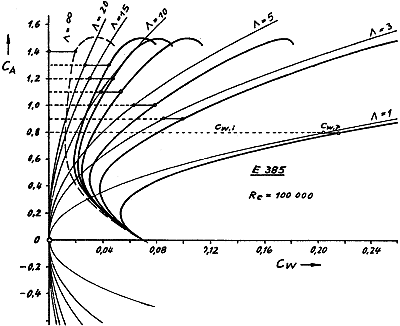
A görbe-sorozatból kétféle ellenállás olvasható le: (vízszintes vonalak)

A folyamatos vonal a profil (alaki) ellenállást,
a szaggatott vonal az indukált ellenállást mutatja

Jól látható hogy l = 1 nél az indukált ellenállást jelző szaggatott vonal hossza kb. 16-szorosa a profil-ellenállást jelentő folyamatos vonal hosszának, míg l = 20-nál ez az arány már csak kb. 1,2 -szeres.
Jól látható az is, hogy l = Ą -nél már csak profil-ellenállás van, indukált ellenállás nincs ! (Ez a görbe az E-385 szárnyszelvény elméleti polárgörbéje!)

Az oldalviszony növelésének korábban szilárdsági okok szabtak határt. Az utóbbi évtizedekben megjelenő műanyagok tették lehetővé a nagy oldalviszonyú szárnyak készítését. Ma már az oldalviszonyt szinte kizárólag az aerodinamikai követelmények szerint lehet megtervezni. Ha az oldalviszony növelésének nincs műszaki akadálya, akkor az oldalviszony úgy növelhető hogy a Reynolds szám még kedvező értéken maradjon.

Az oldalviszony növelésével az indukált ellenállás csökken, de a profil (alaki) ellenállás nő. E kettő között kell megtalálni a helyes középutat (l opt.) Optimális oldalviszony esetén a szárnyszelvény hosszának csökkenése miatt keletkező profil-ellenállás növekedés éppen kiegyenlíti az indukált ellenállás csökkenését. Az oldalviszony további növelése már értelmetlen lenne, mert a kétféle ellenállás összege ekkor újból növekedni kezd.

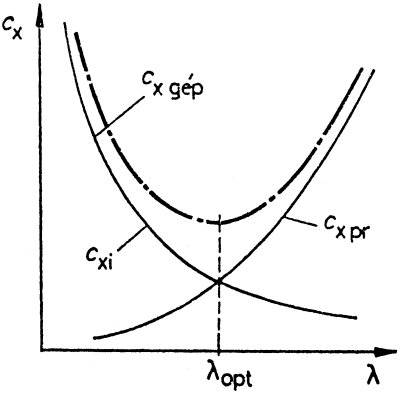
A szárny alaprajza és az indukált ellenállás

Az ábrán látható szárny-alaprajzok nagy modellekre vagy vitorlázó gépekre jellemzőek, de az alakjuk változásából eredő különbség kisebb modellekre is érvényes.

A jelölés ugyanaz, mint az előző ábrán:

A C_y a felhajtóerő-tényező
a Cxi az indukált ellenállás tényezője

A két ábra között a hvég/htő a szárny végén lévő szelvény hossza aránylik a szárnytőben lévő szelvény hosszához, - téglalap szárny esetén a kettő megegyezik, tehát a hányados értéke = 1.

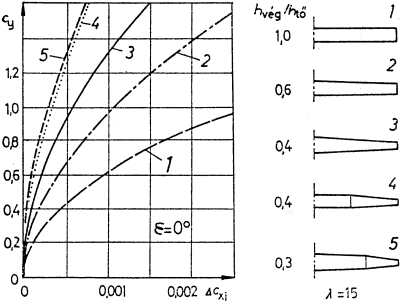
A repülőmodelleknél használatos szárny-alaprajzok (felülnézetek)

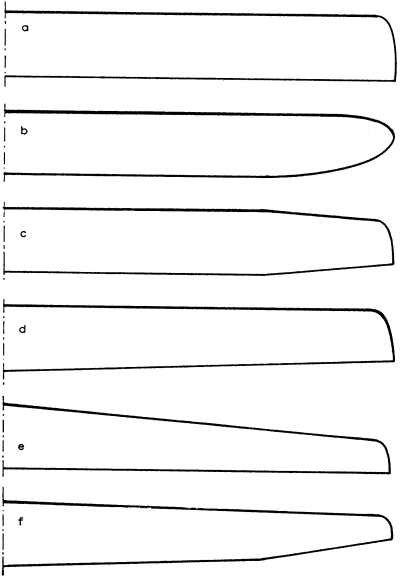
Az indukált ellenállás szempontjából a legkedvezőbb lenne egy ellipszis alaprajzú szárny. Ennek elkészítése több gondot okoz mint a várható előnyök, ezért nem terjedt el. Az ellipszis adta előnyöket - elsősorban kezdetben - sokan alkalmazták téglalap szárny-ellipszis lekerekítés összeállításban.

Ennek előnye nem csak az indukált ellenállás csökkentésében jelentkezett, hanem az ellipszis csökkenő részén alkalmazott szárnyszelvények is változtak.

A szárnyvég kiképzése és az indukált ellenállás

A szárnyvég kiképzése áll:

a szárny végének elcsavarásából és
a szárnyvég lezárásából (befejezéséből)

Az elcsavarás - negatív irányba - azt jelenti hogy a szárny a végeinél kisebb állásszöggel repül, mint a “középső” részén. A kisebb állásszög következtében kisebb a felhajtóerő, de kisebb az ellenállás is, a kettő együtt okozza az indukált ellenállás viszonylagos csökkenését.

Az elcsavarás lehet mechanikus - amikor a bevonat kifeszítésekor adunk kisebb állásszöget a szárny vége felé. (A kilépőlécet felfelé csavarjuk)

Jobb megoldás - de kétségtelenül sokkal több munkát kíván a tervezőtől - ha a szárny vége vastagabb - a szimmetrikushoz közelítő - szelvényből áll, és az átmenet fokozatos. ez a szelvények egyenkénti tervezését kívánja meg. Ekkor az elcsavarás aerodinamikai.

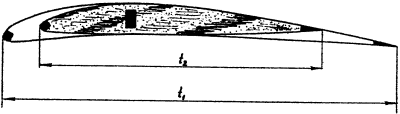
Egymásra rajzolva az eredeti és a lekerekítés végén lévő utolsó szárnyszelvényt jól látható hogy az utolsó szelvény vastagabb (a hosszához viszonyítva) és a szimmetrikus szelvényekhez közelít.

Távlati képen ez így jelentkezik: (a szárnyszelvény hossza a rajzon nem csökken)

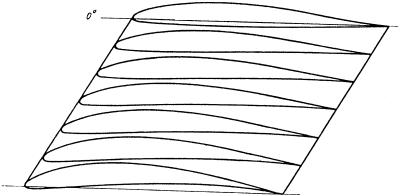
Az elcsavarás - szándékunkon kívül is - létrejön a szárny végeinek “feltörésével” Ennek a “feltörésnek” elsősorban a modell stabil repülése érdekében van szükség,

A modell “bedőlése” esetén a fél-szárnyak vízszintes vetülete megváltozik. A bedőlés irányába eső fél-szárny vízszintes vetülete nagyobb lesz mint a másiké. A vízszintes szárny felhajtóereje nagyobb lesz mint a - törés következtében - kisebb vízszintes vetületű felének, ezért a nagyobb F1 felhajtóerő segíti a modellt a normális repülései helyzetbe visszatérni.

Vízszintes repülés: F1 = F2

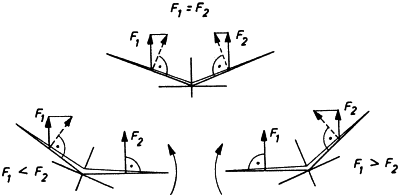
de a törésben lévő szárnyszelvények - anélkül hogy ezt szándékosan tennénk - kisebb állásszöggel repülnek, mint a vízszintesen repülő középrész szelvényei.

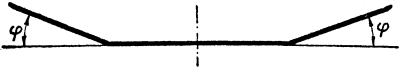
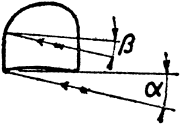
Bebizonyítható hogy a fül állásszögének tangense

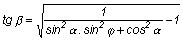
ahol

a = a fül állásszöge
b = a szárnyközép állásszöge és
j = a fül feltörése fokban

Ha a szárnytörés teljesen egyenes, akkor j = 0 ° és nyilván a = b , (az állásszög végig egyforma.)
Ez kiderül a képletből is, mert j = 0 ° helyettesítéssel

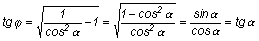
tehát b = a
Ha a = 0° akkor bármilyen feltörés esetén b is 0° -al egyenlő:

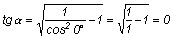minden más esetben b > a

Ezt meggondolással is helyesnek találhatjuk: ha j = 90° (határeset, ha a fül teljesen függőlegesen áll) akkor b = 0° az a bármilyen értékénél l! Ha viszont j = 0° (azaz nincs törés) akkor b = a .
Ha a fül törése 0° és 90° közé esik, akkor a szelvények állásszöge - b - is a 0° és a értékek között lesz, tehát b mindig kisebb, mint az a .
Ez azt jelenti hogy a feltört fül nem csak az oldalirányú egyensúly biztosítása érdekében szükséges, hanem egyidejűleg elcsavarásnak is megfelel. A geometriai és az aerodinamikai elcsavarás mellett ez a szárny elcsavarásának harmadik módja

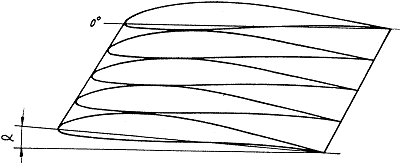
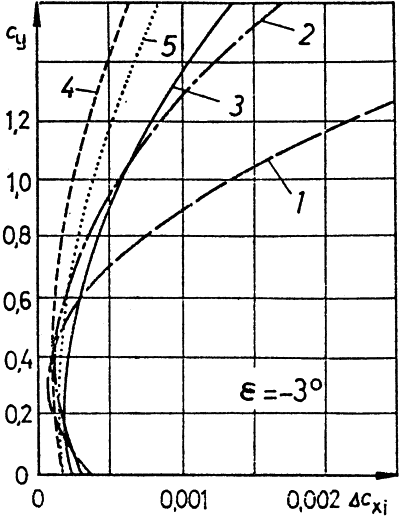
A megfelelő mértékben elcsavart szárnynál az ellenállás is mérhetően javul. A szárny felülnézetének kiválasztásakor bemutatott szárnyak ellenállás-felhajtóerő görbéi -3° elcsavarás esetén így változtak: (az elcsavarás nélkül mért értékek a 33. oldalon)

Az elcsavarásokon kívül a szárnyat valamilyen megfelelő módon kell “befejezni”. Erre láthatunk néhány példát a következő ábrákon:

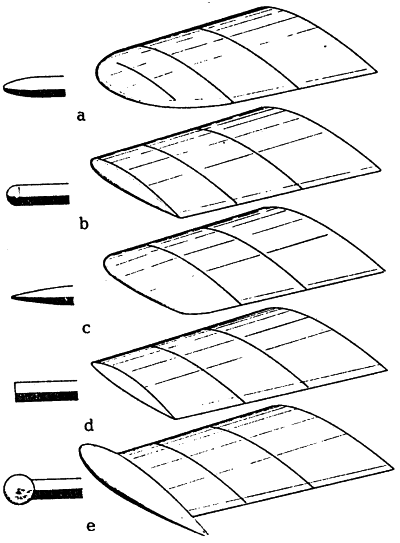
a) a lekerekítések egyik módja,
b) egy záró borda legömbölyítése,
c) az utolsó borda síklappá alakul,
d) a szárnyszelvény vége merőlegesen elcsiszolva,
e) Örvényorsó az utolsó borda végén

Az utóbbi időben a szárny végén különböző alakú zárólapokkal igyekeznek az indukált ellenállást csökkenteni. Ezek a megoldások:

a szárnyvéget (körív mentén) felfelé “kanyarítják”
a szárnyvéget (körív mentén) lefelé “kanyarítják”
A szárnyvégen felfelé és/vagy lefelé nyúló lapokat helyeznek el.

A profil-ellenállás és a Reynolds szám

Ha ugyanazt a szárnyat különböző sebességgel fújják meg a szélcsatornában, különböző Reynolds számhoz tartozó értékeket tudnak mérni. A mérések során arra a következtetésekre jutottak hogy magasabb Reynolds számok esetén a szárnyak ellenállása csökken - a görbék közel párhuzamosak, csak balra - a kisebb ellenállást jelentő értékek felé - eltolódtak

Az előző összefüggések alapján számítsuk ki, hogy egy ellipszis alaprajzú szárny mennyivel jobb egy téglalap alaprajzú szárnynál.

Példa:

A modell adatai:

fesztáv: 2,6 m.
oldalviszony: 1:11
felületi terhelés: 17 N/m²

Siklóméréssel megállapítottuk hogy a modell 6,5 m/s sebességgel repül.
1 : 11-es oldalviszony mellett a szárnyszelvény átlagos hossza 2,6:11=0,236 m. = 236 mm.
A felhajtóerő-tényező nagysága a súlyerő és a felhajtóerő egyenlősége alapján számolható, a repülési sebesség ismeretében:

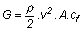amelyből a c_f - felhajtóerő-tényezőt kifejezve:

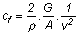
ahol:
r = a levegő sűrűsége 1,25 kg/m3,
v = siklósebesség: m/s,
G = súlyerő: N
A = szárnyfelület: m2,
G = a modell tömege: kg, így:

c_f =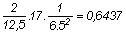

mértékegységre ellenőrizve:

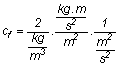
A mértékegységeket egyszerűsítve mértékegység nélküli szám marad,

tehát c_f » 0,64