A modellrepülés elmélete
Bevezetés
A Modellrepülés elmélete
című könyvet “Összeállította: Magyar Modellező Munkaközösség”, megjelent
azokban a 60-as években, amikor Benedek György nem tartozott az akkori modellező
vezetők kedvencei közé, de elméleti tudását sem tudták nélkülözni. A könyv
szerzőjének inkább nem írtak senkit, mintsem a valódi szerző neve megjelenjen a
könyv elején. A könyv fogalmazásából és tartalmából szerzője egyértelműen
meghatározható volt akkor is, és - akiknek még van a könyvből - azóta is.
Közben eltelt néhány év, modellezők részére íródott hazai
elméleti könyv azóta sem jelent meg. Az SI rendszer (Systéme International
d’Unités) 1980-ban történt bevezetésével egyes mértékegységek megváltoztak. Ha
még megtalálható a könyv valahol akkor is előfordulhat hogy valakinek ez a változás
nehézséget okoz. Ezért határoztam el, hogy - a szükséges átszámítások
elvégzése mellett - néhány folytatásban közzéteszem.
Rövidítve, mert az általános,- és középiskolai fizika tárgyak
anyagának magyarázatát elhagyom, azt sokkal jobban teszik a jelenleg forgalomban lévő
tankönyvek.
Az említett könyvből vett idézeteket, a szó szerint átvett
részeket dőlt betűvel írom)
Akadnak olyan modellezők, akik csak gyakorlati tapasztalataik alapján
építenek gépeket és hiábavalónak vélik a számítások végzését. Itt kell
elismernünk hogy a tiszta elmélet önmagában édeskevés egy komoly modell
tervezéséhez vagy beállításához, de az is világos hogy az a modellező képes a
legnagyobb eredmények elérésére, aki kellő gyakorlati tapasztalat mellett elméleti
tudással is rendelkezik. Az elmélet megfelelő gyakorlattal párosulva csodákra képes.
Vegyük most sorra azokat a mechanikai alapfogalmakat és
törvényeket, amelyeknek ismerete a továbbiakban elengedhetetlenül fontos.
Alapfogalmak
Mértékegységek - a
nemzetközi mértékegység-rendszer (SI-alapegységei. (az MSZ 4900/1-78 alapján.)
Alapegységek
(részlet a szabványból)
| |
A
mennyiség |
Az
SI egység |
Sor
szám |
neve |
jele |
dimenziójele |
neve |
jele |
I. |
hosszúság |
l |
L |
méter |
m |
II. |
tömeg |
m |
M |
kilogramm |
kg |
III. |
idő |
t |
T |
másodperc
(szekundum) |
s |
Önálló nevű származtatott SI egységek
(részlet a szabványból)
A
származtatott |
A
származtatott egység |
mennyiség
neve, jele |
neve |
jele |
kifejezése
más egységekkel |
erő, F |
newton |
N |
1N = 1kg.m/s2 |
nyomás * p |
pascal |
Pa |
1Pa = 1N/m2 |
munka,
energia** W, L |
joule |
J |
1J = 1N.m |
teljesítmény,
P |
watt |
W |
1W = 1J/s |
* a nyomás és a mechanikai feszültség
egysége
** a munka, energia és a hőmennyiség egysége
A legfontosabb különbség: A súly
és a tömeg.*
(Akinek részletesebb magyarázatra van szüksége, olvassa el Dr.
Benedek György: Erő-súly-tömeg? Értsük meg a lényeget! című írását az előző
oldalon)
A súly erőmennyiség. (A föld vonzóerejét fejezi ki.)
Az erő (F) az m tömegnek és az a
gyorsulásnak a szorzata:
F = a.m
A súlyerő (G) pedig az m tömegnek és a g
nehézségi gyorsulásnak a szorzata:
G = g.m
A gyakorlatban a tömeg és a súly fogalma még most is keveredik.
Helytelen ilyeneket írni, hogy: súlya: kg: raksúlya: kg, önsúlya: kg, Helyesen így
írhatjuk: tömege, kg, a rakomány tömege, kg. . . stb.
Korlátozás nélkül használható, nem SI egységek:
· a
térfogat, űrtartalom egysége, a liter (l),
· a síkszög egysége,
a fok (o), az ívperc (‘), az ívmásodperc (“)
· a tömeg
egysége a tonna (t)
· az idő egysége
a perc, (min) az óra (h), a nap (d), a hét, a hónap, az év.
· a sebesség
egysége a kilométer per óra (km/h)
· a hőmérséklet
egysége a Celsius fok (oC)
· a munka és energia
egysége a watt. óra (W.h)
A fizika könyvekből ismerni kell a
következő fogalmakat és jelöléseket
A tér és az idő mennyiségeinek neve és jele. (ABC - ben)
(részlet a szabványból)
Átmérő |
D, d |
m |
Felület,
terület |
A, (S) |
m2 |
Gyorsulás
(általános) |
a |
m/s2 |
Gyorsulás
(nehézségi) |
g |
m/s2 |
Hosszúság,
távolság |
l, (L) |
m |
Idő,
időtartam |
t, t |
s |
Keresztmetszeti
tényező |
K |
m3 |
Kerületi
sebesség |
u |
m/s |
Köbtartalom,
térfogat |
V |
m3 |
Lökethossz,
úthossz |
s |
m |
Magasság,
mélység |
h |
m |
Sebesség
(általános) |
v, (c) |
m/s |
Sebesség
(kerületi) |
u |
m/s |
Sebesség
(viszonylagos) |
w |
m/s |
Síkidom
elsőrendű (statikai) nyomatéka |
S |
m3 |
Síkidom
másodrendű nyomatéka |
I |
m4 |
Síkszög |
a , b , stb |
rad |
Sugár |
r, R |
m |
Szélesség |
b |
m |
Szöggyorsulás |
a , (e ) |
rad/s2 |
Szögsebesség |
w |
rad/s |
Távolság,
hosszúság |
l, L |
m |
Terület,
felület |
A, (S) |
m2 |
Térfogat,
köbtartalom |
V |
m3 |
Térfogatáram,
(térfogatáramlás) |
qv |
m3/s |
Úthossz,
lökethossz |
s |
m |
Vastagság |
d, d |
m |
Az általános mechanika
mennyiségeinek neve (ABC - ben)
(Csak azok a mennyiségek, amelyek
számításaink során előfordulhatnak.)
Forgatónyomaték |
M |
N.m |
Hajlítónyomaték |
M |
N.m |
Hajlítószilárdság |
s Bh |
Pa |
Hatásfok |
h |
1 |
Helyzeti
energia |
Ep,
U |
J |
Mozgási
energia |
Ek,
K |
J |
Normális
(húzó, nyomó) feszültség |
s |
Pa |
Nyírószilárdság |
t ny |
Pa |
Nyomószilárdság |
s v |
Pa |
Nyúlás |
e , e |
1 |
Súlyerő |
G |
N |
Súrlódási
tényező |
m , (f) |
1 |
Sűrűség |
r |
kg/m3 |
Szakítószilárdság |
Rm |
Pa |
Térfogattömeg |
r m |
kg/m3 |
Tömeg |
m |
kg |
Légerőtani alapfogalmak
Bernoulli törvénye:
A legegyszerűbb kísérlet: két - enyhén görbített - lap közé
fújva, azok összezárulnak, pedig az ember azt gondolná, hogy a rájuk fújt levegő
nyomása azokat széjjelnyomja
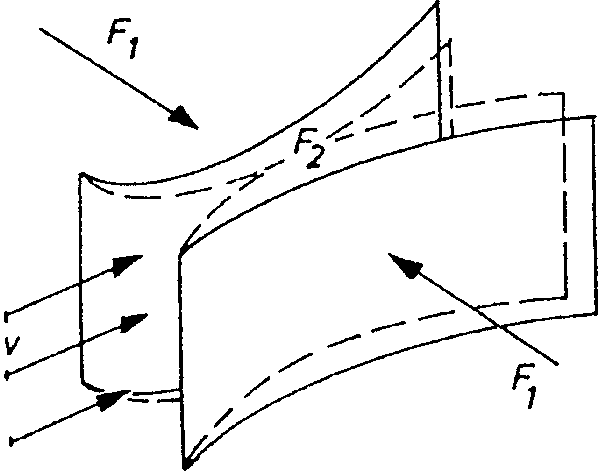
A két lap egymáshoz közelít
Az áramló folyadék (és gáz) sebessége és nyomása közötti
összefüggést Bernoulli (Daniel, svájci fizikus, 1700-1783) állapította meg. Az
összefüggés az áramló folyadékokra (és gázokra) alkalmazott energia megmaradás
törvénye.
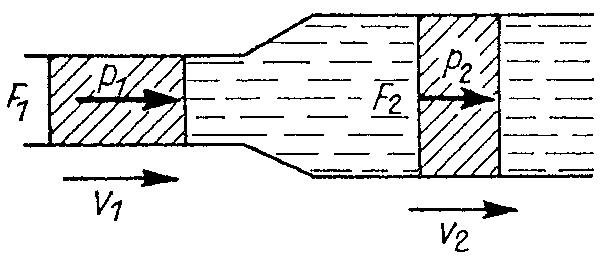
Vízszintes csőben áramló folyadék
A folyadék sebessége a cső A1 keresztmetszetében v1,
az A2 keresztmetszetében v2
Áramlás esetén “t” idő alatt az A1 keresztmetszeten A1.v1.t,
az A2 keresztmetszeten A2.v2.t térfogatú
folyadék (gáz) áramlik át. Az áramlás folytonosságának tétele szerint ez a két
térfogat egyenlő, tehát
A1.v1.t = A2.v2.t = V
Áramlás közben a folyadék nyomásából származó erők munkát
végeznek.
Ha az A1 keresztmetszetnél a nyomás p1, A2
keresztmetszetnél a nyomás p2, akkor a “V” térfogat “s”
elmozdulásakor a “p” nyomásból származó erő által végzett munka (L)
L1 = p1.A1.s1 = p1.A1.v1.t
= p1.V
L2 = p2.A2.s2 = p2.A2.v2.t
= p2.V
A nyomási munka különbsége
L1 - L2
az “m” tömegű folyadékmennyiség mozgási energiájának
megváltozásával egyenlő.
A mozgási energiák: (E)
E1 =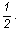 m.v m.v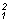 , és
E2 = , és
E2 =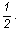 m.v m.v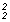 , vagyis ezek különbsége , vagyis ezek különbsége
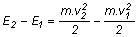
az energia megmaradásának törvénye szerint tehát
L1 - L2 = E2 - E1, illetve
L1 + E1 = L2 + E2,
akkor behelyettesítve a korábban kapott kifejezéseket
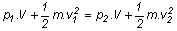
Osszuk el az egyenlet mindkét oldalát “V”-vel és az “m”
(tömeg) helyére írjuk be a sűrűség (r ) értékét
p1 + 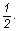 r .v r .v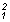 = p2 + = p2 + 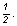 r .v r .v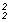
Ezt az összefüggést Bernoulli tételnek nevezzük.
Ebben az egyenletben “p” a statikai nyomás, az 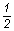 .r
.v2 kifejezés, - amelynek számértéke a térfogategységben lévő folyadék
(gáz) mozgási energiája - szintén nyomás jellegű fizikai mennyiség, a neve
dinamikai (vagy torló) nyomás. .r
.v2 kifejezés, - amelynek számértéke a térfogategységben lévő folyadék
(gáz) mozgási energiája - szintén nyomás jellegű fizikai mennyiség, a neve
dinamikai (vagy torló) nyomás.
Bernoulli tétele szerint, ha a folyadék (gáz) vízszintes csőben áramlik, akkor a
statikus és a dinamikus nyomás összege - az össznyomás - a cső minden pontján
ugyanaz.
A tételből következik hogy kisebb keresztmetszeteken az áramlás sebessége nő, a
folyadékban (gázban) uralkodó nyomás csökken, és megfordítva.
A statikai nyomás
-
“p” - felületegységre ható erő. Nyugalomban lévő folyadékok (gázok)
nyomását nevezzük statikai nyomásnak.
Dinamikai - torló - nyomás:
Repülőgépeknek a körülöttük lévő levegőhöz viszonyított
sebessége az un. Prandtl - csővel határozható meg.
A cső “A” nyílásánál megáll a levegő (mert az “U” alakú
csőben lévő folyadékot - egyszerűbb számítás kedvéért vizet) - felnyomja a cső
másik szárába, amelynek nyílása a mérőcső oldalán helyezkedik el. Az “A”
pontban (ezt a pontot torlópontnak nevezzük) hat a levegő p1
nyomása, a “B” pontban a v sebességgel a cső mellett áramló levegő p2
nyomása. Az “U” csőben a folyadékok szintje közötti különbség - mint
nyomásmérő - a két nyomás különbségét mutatja.
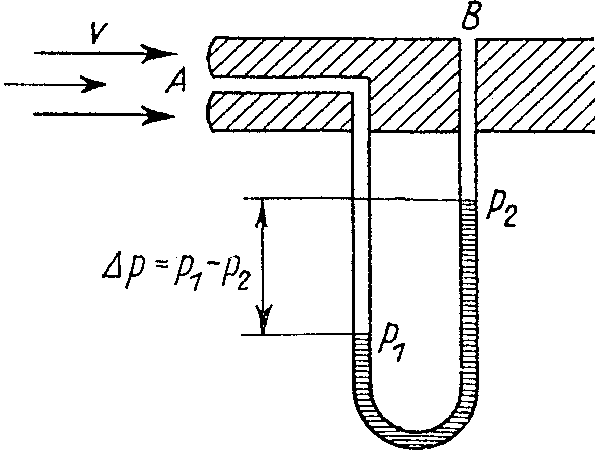
A Prandtl-cső
Példa:
Legyen a p1 - p2 = 100 mm = 0,1 méter. Ilyen magas vízoszlop
nyomása 1 m2 felületre 100 kg/m2 = 1000 N/m2 = 1000
kg/m.s2
A levegő sűrűsége 1,25 kg/m3, tehát a
p1 - p2 = 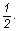 r .v2 r .v2
kifejezésből a sebesség:
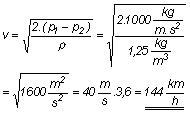
Bernoulli törvénye akkor lenne maradéktalanul érvényes, ha az
áramló közeg és a cső - vagy az áramló közeg és az útjában lévő test(ek)
között nem lenne súrlódás.
A közegellenállás
Ha valamilyen közegben (pl. vízben vagy levegőben) egy test mozog -
vagy nyugvó test esetén körülötte a közeg áramlik - a test és a közeg között
kölcsönhatás lép fel. A közeg a testre a mozgás irányával ellentétes irányú
erőt fejt ki. Ezt az erőt közegellenállásnak nevezzük.
Ezen kívül számításba kell venni a test és a közeg közötti
súrlódásból származó ellenállást is. A közegellenállás tehát összetett
erőhatás. Kísérletekkel állapították meg hogy a közegellenállás nagysága
(F) egyenesen arányos a testnek a mozgási irányra merőleges legnagyobb
keresztmetszetének területével (homlok-felületével), (A), a közeg sűrűségével (r ), a közeg és a test közötti viszonylagos sebesség (w)
négyzetével, és függ egy mértékegység nélküli alaktényezőtől (c)
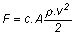
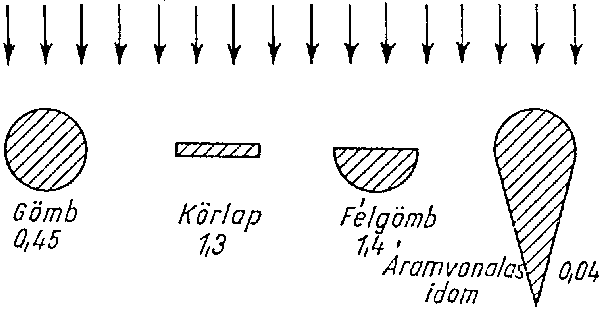
Külömböző testek alaktényezője
Kis sebességek esetén számolni kell a határrétegben fellépő
súrlódás hatásával is.
Amikor a levegő a testet “körüláramolja”, azok a részecskék,
amelyek a test felületével közvetlen érintkezésbe kerülnek nem siklanak végig a
felületen, hanem rátapadnak, mintegy burokként veszik körül. Ezáltal az áramlás
közvetlenül a test felületén lefékeződik, sebessége itt “0”, és a szabad
áramlás a “v” sebességre egy aránylag vékony rétegben gyorsul fel. Modellezés
során előforduló sebességek esetén e réteg vastagsága kb. 1 mm. lehet. Ezt a
réteget Prandtl göttingai egyetemi tanár után nevezzük “határréteg”-nek.
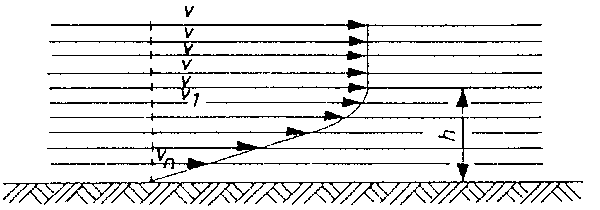
A határréteg
Az ábrán úgy képzeltük el, mintha a rétegek további
levegőrétegekből állnának, mindegyik réteg sebessége valamivel több mint az alatta
lévőé, egészen addig, amíg a legkülső réteg sebessége már megegyezik az áramló
közeg sebességével.
Prandtl kutatásai derítettek fényt arra hogy a levegőnek a
határrétegben való viselkedése döntő hatással van az ellenállásra.
A test körüli áramlás tehát két részre osztható: a test
közvetlen közelében a teljesen a felülethez tapadó, álló határrétegre, és a
határrétegen kívüli, gyakorlatilag súrlódásmentes részre. A test körüli
nyomáseloszlást ez utóbbi határozza meg, mert a határrétegben a nyomásváltozás
akadálytalanul érvényesül.
Az alaktényezővel kifejezett ellenállás két részből áll:
a nyomási vagy alaki ellenállásból, és
a súrlódásból származó ellenállásból
A határrétegben keletkező súrlódási ellenállás nagysága a
határréteg áramlásának jellegétől függ. Az áramlás jellege lehet:
lamináris - réteges áramlás, vagy
turbulens - gomolygó áramlás

Lamináris áramlás
A lamináris határréteg ellenállása kisebb a turbulensnél, viszont
erősen befolyásolja a felület minősége. Durva, szemcsés felület nem kedvez a
lamináris áramlásnak. Kis sebességeknél az áramlás mindig laminárisan indul és a
test mentén - bármilyen legyen az áramlás - a határréteg egyre vastagabbá válik. A
határréteg vastagodása okozza azt, hogy a test mögött keletkező örvénylés sokkal
nagyobb ellenállás-növekedést okoz, mint amennyit a felületi súrlódáson
csökkenteni lehet.
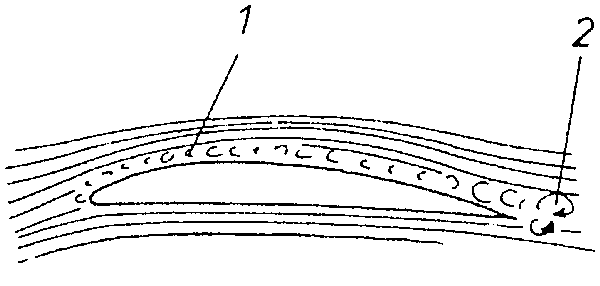
Turbulens áramlás
Bár a turbulens határréteg nagyobb felületi súrlódást jelent, az
ellenállás mégis csökken, mert az ellenállás legnagyobb részét jelentő
örvénylés sokkal kisebb.
A turbulens határréteg a külső - határrétegen kívüli -
áramlásból is képes mozgási energia felvételére, az áramlások keverednek, az így
megnövekedett energiájú turbulens határréteg tovább marad a felületen, mint a
lamináris.
Kis és közepes sebességű áramlás esetén a határréteg mindig
laminárisként indul és csak később lesz belőle turbulens. Azt a pontot, ahol az
áramlás képe változik, átváltási pontnak nevezzük.
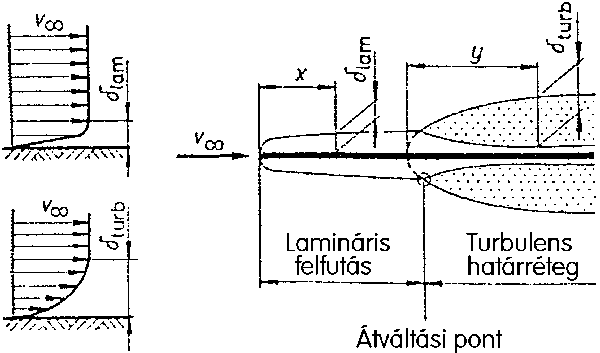
Az átváltási pont
Ez általában a szárnyszelvény legvastagabb pontján következik be.
A határréteget mesterségesen is turbulenssé lehet tenni, a szelvény elején
alkalmazott “turbó szál” felszerelésével.
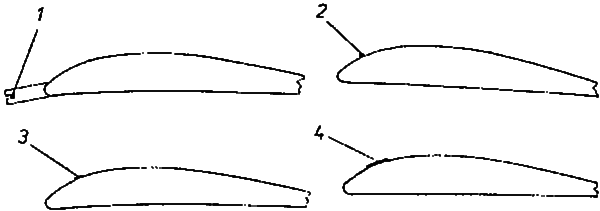
A „turbó szál" elhelyezése
Ívelt felületű test - áramvonalas szárnyszelvény - körül az
áramlásnak két szakaszát különböztethetjük meg: A szelvény legvastagabb pontja
előtt az áramlás gyorsuló, mögötte lassuló. Az áramló levegő nyomása a
gyorsuló szakaszban csökken, a lassuló szakaszban növekszik.
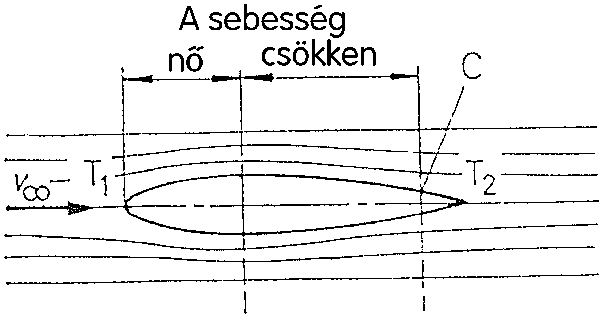
Az áramlási sebesség változása
A lassuló szakaszban a felület közelében futó áramvonalaknak
nyomásnövekedéssel szemben kell haladniuk. Az áramlás mozgási energiájának
csökkenése miatt a felületi súrlódás a levegőrészecskéket megállítja. Az utána
jövő részek ezeket nyomják, itt a részecskék a felülettől elválnak, az áramlás
“leszakad” a felületről. A leválási hely mögött örvény keletkezik, amely egyre
növekedve marad el a test mögött.
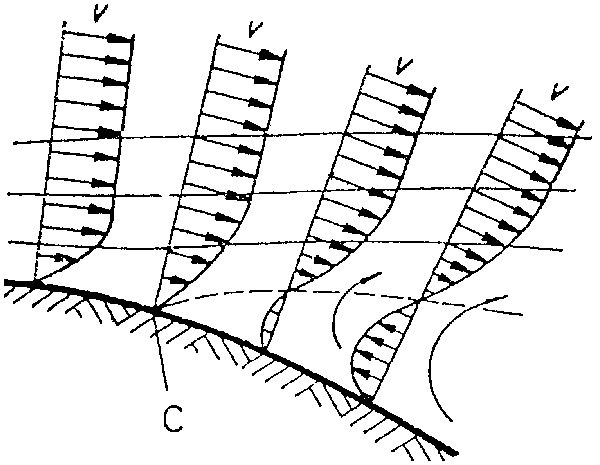
A visszaáramlás a határrétegben kezdődik
|


